さて、今回は３年生の進化の記事の続きです。

 

４ｍｘ９４

ここは何でも屋さんです。ここでは、お星さまと黄金たこ焼きが良く売れます。お星さま２個と黄金たこ焼き３個では190,000,000ユーロ、お星さまと黄金たこ焼き5個では310,000,000ユーロです。では、黄金たこ焼き１個はいくらでしょうか。

 

突如出て来る、この物凄い数を見て、子どもたちが

「えーっ！」とか「何ー！」とか言うのが楽しみな

ちょっと意地悪などんぐり先生ですが・・・。

 

 

その後、約半年後に再挑戦してみました。

 

黄金たこ焼きがお月様に変わっていますので、悪しからず。

 

 

まず、お星さま2個とお月様3個が190,000,000ユーロなので、

310,000,000ユーロから引いた残りの120,000,000ユーロが

お星さま1個とお月様２個の値段としました。 

今度は、190,000,000ユーロから120,000,000ユーロを

引いた残りの、お星さま1個とお月様１個が70,000,000ユーロ

となりました。

 

 

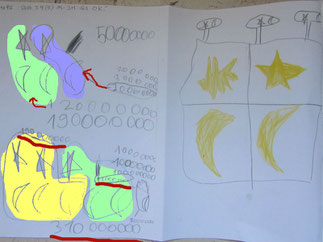
120,000,000ユーロと70,000,000ユーロの違いが

お月様１個分なので、お月様１個は50,000,000ユーロと

なり正解でした。

 

 

 これは、絵を描かなければ絶対に解けない問題です。

なぜなら、計算だけで解こうとすると

連立方程式を使う必要が出て来るからです。

 

連立方程式はまだ習いませんよね。

 

でも、

 

裏を返せば

絵を描いて視考力を使うと

小学3年生でも以外に簡単に解けてしまいます。

 

中学校2年生の教科書に出てくる問題でさえもです。

 

自力でノーヒントでです。

 

 

そして、これこそが

本物の理解であり思考力なのです。

 

 

連立方程式という便利な道具がないから問題が解けない？！

まだ習ってないから出来ない？!

 

 

視考力を使えば、自分の力で工夫して問題を

解決することができるんです。そしてこれは、

自分を、自分の力を信じるという大きな

財産を子供達に与えてくれます。

 

 

これから先、

ますます多様化し、複雑になっていく社会のなかで

自分を信じ、自分の信念のもとに人間らしい判断をもって

行動できる若者を育てるための第一歩だと考えます。

 

 

是非とも、どんぐり問題をただの算数の応用問題と

考えず、教育とは何か、何のために、子どもたちは

勉強するのかということを、もう一度改めて考え直してみる

ことをお勧めします。

 

テストで高得点をとること

先生や周りの人に高い評価を得ること

有名大学に入ることのために

 

勉強するのではありません。

 

 

自分のために

自分が大切だと思うことのために

自力で一つずつ積み上げていくことの重要性とその楽しさを

人生をかけて味わって欲しいと思います。

 

 

４MX０９

 

カブト3匹とクワガタ4匹を缶に入れて重さを計ったら2㎏600gでした。

缶はカブトと同じ重さで、カブトは3匹とも同じ重さです。また、

クワガタは1匹がカブトと同じで、他の３匹はカブトの丁度半分の

重さです。では、軽いクワガタ１匹の重さは何ｇでしょう。

 

という問題をしました。

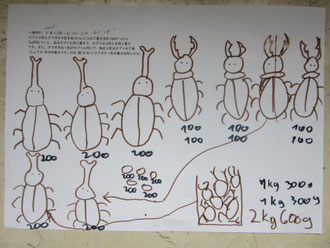
「はい、出来た。1匹200ｇ。」

 

じゃあ、ちょっと待ってね答え確認するからね、

と言って、私も絵を描きながら問題を解く。

 

あれ、半分残ったなー。

どうするこれ？

 

そうだな、2倍にすればいいか。

 

ということで、カブトが６匹分＋クワガタが1匹分

を2倍にして、カブト13匹分で５㎏200ｇということにして、

カブトが４00gとでました。

 

ですから、軽いクワガタはその半分で200g。

 

 

その後、

 

子どもの解答を見て、

ちょっと意味が分からなかったので、

 

「なんで、クワガタ200ｇって分かったの？」

 

「だって、クワガタが13匹分だから・・・

2kｇ600ｇを半分にしたら、１㎏300ｇ

だから、100ｇ二つ分。」

 

 

なるほど～。気が付かなかった。

 

私はカブトを基準にして考えた。だって１だから。

子どもはクワガタを基準にして考えた。半分を。

 

半分を基準に考えれるって凄いな。

 

 

そうだよね、クワガタを基準にしたほうが、簡単だし、速い。

 

 

そして、説明してもらうまで、クワガタを基準にすることを

思い付けなかった自分の頭の固さ

 

そして、子どもの頭の柔軟さと合理性

 

恐れ入りました。

 

 

 

3mx40

クジラのマッコウ君の今日の朝ご飯はプランクトンです。赤プランクトンと青プランクトンを合わせると12428匹います。赤プランクトンは青プランクトンの丁度12倍だとすると、赤プランクトンと青プランクトンは、各々何匹いるでしょう。

 

The key of this problem is that the red planktons are as 12 times as the blue plankton s. It is important that children understand this part well and drow it.

 

Please look at this picture.

 

 

He wrote 12 in spite of drawing 12 circles. And what happens next is to devide 12428 by12without understanding correctly the problem. And he repeats to calculate foever but of course he can’t reach the correct answer.  The number 12 he wrote became the obstacle and it deprives of his understanding and thinking.

 

That they draw tiny parts from the problem precisely even if it doesn’t seem to be important should be the turning point that they can find a solution or not.

 

 

However, how about they drow it like this.

 

While they are looking this picture carefully, they will find that they can distribute 12428 planktons for each circle. And the number of the circle is 13.

 

This seems small and unimportant thing but it will make a big difference to their understanding and thinking.  

 

The same thing will happen to reading ability. 国語の文章読解でも同じです、分

かっているようで分かっていないのは、このような細かなところが正確にイメージ化出来ていないからなのです。

 

 

So that, firstly, they need to get used to draw as said in a sentence of the problem(original visual imaging): this is understanding and secondly they need to look at it carefully and to operate the images for the solution that they are asked(operation of visual images): this is thinking. That’s how, they can find out the answer sooner or later. Or we can also say the solution pops out automatically. Because they will see it on the paper.

 

 

また、絵を描く理由ですが、頭の中の視覚イメージを大量に長時間保持しておくのは大変なエネルギーを要します。それでは、イメージ保持だけで精一杯で、それを使って思考するのは困難です。ですから、紙に描くのです。そうすることで、視覚イメージ保持に使われるエネルギーを全て考えることに使えますので、少ないエネルギーで多くの思考が可能になるというわけです。