3年生 進化の様子
進化1 足し算だけでも解ける!
さて今日の問題です。
絵ではクジラが亀になっていますが
悪しからず。最近うちで亀を飼い始めたもので・・・
3mx56
進化2 倍数問題は板についたようです

3MX79
進化3 単位や量は実感することが大事

3mx59
蟹の介は一歩で25mm、蟹の心は一歩で30mm歩くことが出来ます。二人は、お母さんに頼まれてお使いに行くことになりました。蟹の介は15cm離れている魚屋さんへ、蟹の心は12cm離れたパン屋さんへ行きました。二人が、家を出て帰ってくるまでには、どちらが何歩多く歩くことになるでしょうか?
介が4歩多い 正解!
この問題はかばんから物差しを出してきて
絵を描きました。
上のほうが心で
下が介ですね。
家を出て帰って来るというところも
ちゃんと絵を描けば
往復分計算しないといけない
ということも目で見えますので
忘れることもありませんよね。
たまに、
うっかり単位を間違えて書いちゃったって
いうことがあるかもしれませんが、
それは
例えばmm、cm、mといった記号と実際の長さに実感が伴っていない
からかもしれません。
日頃からイメージを通して
長さを意識して実感するようにすると
うっかり、mとcmを間違えて書いちゃった
などは起こりえないと思います。
うっかりミスや
ケアレスミスは
実はうっかりではないのです。
丁寧にする癖がついているか
ちゃんとイメージ出来ているか
うわっすべりの理解でやっていないか
嫌々やらされていないか
沢山の量を作業的に勉強していないか
そういう日頃の学習態度や生活態度の
総括がうっかりミス、ケアレスミスですので、
ケアレスミスが多い場合は
しっかりと対応して治していく必要があります。
コーヒーブレイク
車で移動中のある日、
お父さんが子供に遊び半分で以下の質問をしました。
144個の飴があります。12人の子供に同じ数ずつ分けると
一人何個ずつ貰えますか?
5秒程して、
12と答えました。
私は、12人の子供の12をただ繰り返して言ったの
だろうと思いつつ、
どうして12個になるのか
聞いてみました。
すると、その5秒くらいの間に
彼の頭の中で
以下のようなことが展開されていたそうです。
まず、10個の飴のまとまりが14個とあと4個
次に、子供が12人いる所がイメージされました。
10個の飴のまとまりを12人に分配すると
残り24個
そこで、最後に2個ずつを12人に再分配して
12個ずつとなったそうです。
すげー、視考力めっちゃ使ってるーって思いました。
例えば、私の様に
手順を教えてもらって答えを導き出すように
教えられた子供は
この質問を聞いた瞬間に、
以下のような反応をするはずです。
そして、
144÷12を頭の中で計算出来る子供か
12×12=144というのを覚えていた子供は
口頭のみで正解にいたることが出来ます。
確かに上記の二つのパターンとも
正解は正解です。
しかしながら、
この二つのプロセスは雲泥の差、
天と地との差があるのがお分かりいただけるでしょうか?
理解力と応用力がまるっきり違います。
この問題のように
計算問題を単に文章にしただけの
簡単な問題であればまだ
良いですが、
もっと複雑な問題になると
計算だけ出来ても
応用力がないため
行き詰ることは目に見えています。
私自身
自分の子どもが小さい時に
どんぐりの先輩ママのコメントなどを
拝見していて、
お子さんたちの進化の記事を
読んで自分の子供もこんな風に
なれたらいいなぁなんて
半ば半信半疑だったことを
覚えていますが、
今まさにその先輩ママさんたちが
書かれていた記事のような
進化を目の前で体験することが
出来、視考力のすごさを確信することが
出来ました。
どんぐり理論とどんぐり問題には子供達の持って生まれた才能を
発揮する方法が確かにあります。
是非ご家庭で取り組まれることを
お勧めします。
進化4 実は分からん帳行きの方が多いんです~
いろんなところで、子供達のどんぐり問題の記事を書いています。皆さんにどんぐり問題がどのくらい威力があるかということを知っていただくために、正解した問題を掲載していますが、いつも正解な訳ではありません。むしろ、分からん帳行きの問題が多いです。
どんぐり問題は、子どもの学力養成が目的なので、答えはオマケ、あっていようが間違っていようが、問題を解く過程で、本人が自力でイメージ想起をしてそれを動かしていくことが重要なんですよ。とはいっても、正解している問題を見て貰わないと、「ほんとに、そんなんで考える力つくんですか?」「ほんとに、難しい問題を秒殺できるようになるんでしょうか?」と半信半疑ですよね。
ということで、ここに来て、ある程度皆さんにも信用していただけていると思いますので、あえて今日は、進化の舞台裏の様子をお伝えしたいと思います。
問題
朝太郎は、朝のコーヒーを飲んでいるときに、ふと飴を食べたくなり200秒で11個の飴玉を作ることができる自動飴玉製造機を発明しました。それでは、この製造機が2時間で作ることが出来る飴玉の数と、その数の百の位の数字を十の位にして、十の位の数字を一の位にして、一の位の数字を百の位にした数の差はいくつになるでしょう。
一日目

飴玉製造機を一生懸命描いたら、頭が痛くなってきて終了。
二日目
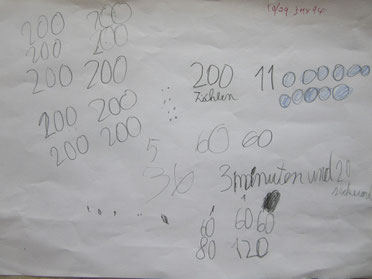
数字を何だかたくさん書いてみたが・・・断念。
三日目

これまた何だか数字をたくさん書きこんで、結構長いあいだ考えていた様子ですが、断念。飴玉の数も正解にかなり近かったのですが・・・粘り負け。
とうことで、もう違う問題したいということになったので、とりあえずこの問題はお蔵入りということになりました。
ま、コメントとしては、数字たくさん書いてますが、全体をパッと見渡せる絵がちゃんと描いてないので、答えに至らないのは当然かな?って感じですね。
やっぱり、時間が入ってくると絵に描き表しにくいようですが、そこを何とか工夫するといいみたいですね。
ということで、正解に至った問題でも、数日かかった、数週間かかった、数か月かかったというものもあります。でも、それが本当の理解力や考える力、そして間違ってもくじけない、諦めない心や、やり抜く根性、そして思考の忍耐力を育てます。最後に、長い時間かかったけど、自力で何とか解けたという何とも言えない、充実感をともなった自信を得ることが出来ます。
進化5 結局なんだかんだ言っても、やっぱり絵で考えないと答えが見えません
問題
サンタさんが、子供10人に、それぞれ同じ値段のお菓子を3個ずつと、そのお菓子1個の丁度2倍の値段がする玩具を2つずつ買ってあげようと思っています。ただし、サンタさんが使えるお金を全部で140ユーロとすると、1個いくらのお菓子と1ついくらの玩具を買ってあげればいいでしょう。

という問題です。文章通りにちゃんと絵を描けました。

それで、あっ、もうこれは解けるかなと思ったら。何か変なことをし始めて
「お母さん、これ難しいよね。」って言い始めました。うーーん!↓
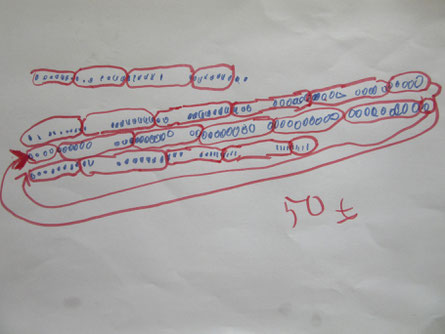
そこで、「難しいも何も、ちゃんと絵は描けてるから、さっき描いた絵をよーく見てごらん。」「よーく、見らたらそんなに難しくないよ。」「だって、もう絵は描けてるからね~。」とアドバイスしてみました。そしたら数分して答えが出ました。
一人、お菓子7個分の値段だから、お菓子が1ユーロとして、7ユーロ。でも一人7ユーロだったら、10人で70ユーロにしかならない。じゃあ、お菓子1個2ユーロにすればいいと考えたそうです。
で、お菓子1個2ユーロ、玩具1個4ユーロ で正解となりました。
そう、まさに、
言葉から正確にオリジナルのイメージ想起が出来る→理解
そのイメージを操作(移動、複写、比較、変形)すること→思考
絵さえ描ければ、あとはそれをじーっとよく見るだけで、全体と部分の関係性が見えてきます。ですから、あとは尋ねられている部分を正確に抽出出来れば正解に至ります。
とにかく、文章通り正確に絵を描くこと、そしてその絵をよーく見ること。
何だかんだ言ってもやっぱりこれが重要です。
進化6 絵を描けばとにかく嫌でも見えるんです、その「答え」が。
3mx問題
ウルトラ君のお小遣いは20ユーロでしたが、この4月からウルトラセブンになるので、15ユーロ増えることになりました。その代わり、今まではお小遣いの半分の半分を食事に当てていましたが、これからは、半分にすることになりました。では、食事代意外に使えるお金はいくら増えた、あるいは減ったことになるのでしょう。

まずは、20ユーロ札を持ったウルトラ君が怪獣を倒しているところを描きました。

次に、お小遣いが15ユーロ増えて、35ユーロ持っている陽気なウルトラセブンを描きました。
今までのお小遣いの半分の半分が5ユーロ →食事代
これからのお小遣いの半分の絵を描きました。
あとは、それ以外を比べると、違いは2.5ユーロ多いと
いうことで正解!
本当に、ただ絵を描くだけ、
たったこれだけのことで皆例外なく考える力がつきます。
天才にもなれますし、いい加減にしても秀才にはなれます。
本当に単純なことなんです。
言葉を聞いて(読んで)自力で絵を描く→理解
描いた絵を操作する→思考
もちろん、絵を描かなくてもイメージを頭の中で保持した状態で
でも考えられますが、なかなか普通の人は頭の中だけで
鮮明にイメージ操作することは難しいので、ただそれを紙に
描くというだけなのです。
紙に書けば、それをイメージし続けることにエネルギーを
使わない分楽になりますからね。
そして、面白いことに
小学3年生問題なのですが、一切計算式を使わなくても書かなくても
問題が解けているというところです。
つまり、計算が出来る事と
考える事ってあんまりリンクしていませんよね。
それは当然なことなんです。
何故ならば、
理解と思考は計算式以前に
存在すべきものだからです。
まず、質問を理解して、考えます。
そして、問われている答えを抽出します。
それが出来たら、
その過程を算数語(計算式)という共通言語で
書き記すというのが正しい順番です。
しかしながら、
みんな最後の計算式の部分だけを一生懸命に
やっているのです。
そして、何でこんな簡単な問題も解けないんだろう?
計算は出来るんだけど、どうして応用問題になると
手も足もでないんだろう?と悩むわけです。
おかしいですよね。
確かに、公式を覚えたり、問題のパターンをある程度覚えれば
答えは出ますし、点数もとれます。ですから、大学入試も
頑張れば突破できるでしょう。が、結局大元の理解力と思考力を
鍛えなければ、本人の頭は当然よくなっていませんし、
問題解決能力も育ちません。
今現在、求められている人材は、高度な問題解決能力をもった
人間だということからしても、
言われたことをただまねして、暗記して乗り切る方法を
教え込まれた子供達はどう考えても求められている人材像とは
かけ離れた教育を受けていることになります。
気付いた人は早速どんぐり問題を始めましょう。
出会った時が初め時、
気付いたときが初め時。
ぼやぼやしている暇はありません、
子供達はすぐに大きくなってしまいます。
進化7 9歳の壁を超えるのは目前!
問題 デンデン君は、毎朝公園の周りのお散歩ロードを1周します。
お散歩ロードは1周200mです。デンデン君は15分で5m進むことが出来ます。では、デンデン君が朝のお散歩意外に使える時間は1日に何時間何分あるでしょう。
まずお散歩ロードの絵を描きました。
200mに5mが何回入っているかだしました。
5mが20個で100mですので、
5mが40個で200mということになりました。
次に、5mで15分かかるので
15分を40個描きました。
15分が4個で1時間になりますので、
4個ずつ丸で囲みました。
ということで、朝の散歩は10時間かかります。
1日は24時間なので、
お散歩意外に使える時間は14時間ということで正解です。
今回も前回同様に、数字がたくさん描かれていますが(笑)
今回はまだ全体が整理させていて数のみながら、
若干分かり易く描かれています。
また、15分を4つずつ囲んで1時間の固まりにする
という工夫をしたことで時間を数えやすくすることが出来ました。
3年生の問題ともなってくると、
数が増えて大変だと思いますが、まだまだ計算式で考えるのではなく
頑張って絵を描いて考えるということをもうしばらく
続けて行って下さい。
つまり、抽象思考が出来るからといって、記号や文字、数字のみで
考えるのではなく、抽象思考の移行期を過ぎるまで(小学校高学年)
いかに具象思考(半具象思考)を続けていけるかということが
大切になってきます。それが、その後の伸びしろを決定するからです。
3年生、つまり9歳の壁を視考力で乗り切ったらあとは
こっちのもの。理解と思考の方法が身についていますので、
そこから、今まで培った理解と視考の過程を
みんなの共通語である算数式で表す練習をしていきます。
それが、4年生頃からです。
そして、5年生と6年生で、自分の理解と思考の過程を
算数語を使って理論立てて説明できるようなプレゼンテーション力も
鍛えて行きましょう。
3年生は正念場!
焦らず、ゆっくり、確実に進めていきましょう。
進化8 ああ、過渡期です・・・
3年生 算数問題 問題番号85
映画館の入り口に35人が並んでいます。先着50名様にプレゼントを渡します。10番目までは特別プレゼントで普通のプレゼントの3倍の値段がします。全体の予算は700ユーロです。では、今、いくら分のプレゼントが残っているでしょう。

映画館ではなく、動物園になっているので悪しからず。
で、絵は描けたんです。で、のこり15個分のプレゼントの値段を
出せばよいことにも直ぐに気づいたんです。
そしたら、また、数を書き出した。

嗚呼~。
ガクッ。って感じです。
一日目は、「絵を描いてちゃんと見ないと分からないよ。」と何回か言って
放っておきました。
案の定、何だかよく分からない数字の羅列で終わって
しまいました。当然ですよね~。
さて、二日目。
「正確に絵を描いて、ちゃんと見ないと分からないよ。」
と釘を刺したのにも関わらず、
嗚呼~。
また数字かよ。
これねぇ~。
ここ最近なんですよね。
以前はなかった現象なんです。
3年生に入って、ここ最近
やたら数字を描くようになったんです。
そして、「難しい、分からない。 」
ってなるんですが・・・。
家庭では、計算は制限していますし、
その他不必要な勉強は一切していませんので、
やっぱり、学校の影響でしょう。
もちろん、学校は大事ですし、否定もしませんが、
学力養成、思考力養成は今の所してもらえませんので、
家庭で修正する必要があります。
ちなみに今学校では、こんな感じのことをやっています。
ということで、
イライラしてきて
横から、その数字の描かれた紙をひったくって、
「こんな余計なことは書かんでよろしいっ。
数字をいくら書いても、一生解けん!!!
最初に書いた自分の絵を良く見て、良く見て
良ーく見て、絵で考えろーーーーー!!!」
と言いました。

すると・・・
30秒もしないうちに。
「あっ、僕、答え見えた。」
って、言って、
かくかくしかじかで・・・・・
と説明を始めて、
150ユーロで正解となりました。
この過程では
計算なんて一つもしていませんよ。
数字だって、一つも書いていません。
ただ良く見ただけです。
そうそうそう、
そうこなくっちゃねー。
それでよろしい。
よく見るってことがどんだけ大事かってことですよ。
今回のことで、本人も、目で解くことがどういうことなのか、
そして、目で解くとどういうことが起こるのかということを、
確実に認識しましたね。
あの、答えが見えたときの嬉しそうな顔!
それですよね。
お宝発見したっ!って顔。
そう、
それが大事。
それが、難問を克服する
モチベーションになると
子供達は一人でに、進化していきます。
ちなみに、どんぐる教室のお友達も
ちゃんと絵を描いて、
「あっ、先生分かった分かった。」って言って、
即答してくれました。
この日、この子は眼鏡が壊れていて
あんまり良く見えなかったにも関わらずです。笑
ハーフの子供達でも、
ちゃんと日本語の内容を理解して、複雑な問題を解けるような
理解力、思考力、読解力がつきますので、
皆さんも是非始められて下さいね。
進化9 チャレンジ精神
先日どんぐる教室で以下の問題を解いてみました。
問題
ここは何でも屋さんです。お月様と黄金たこ焼きが良く売れます。
お星さま2個と黄金たこ焼き3個で、190,000,000ユーロ、お星さま3個と
黄金たこ焼き5個で、310,000,000ユーロです。黄金たこ焼き1個の値段はいくらでしょうか?

何でも屋さんの絵を描いて、190,000,000ユーロ!!!何それっ!
というところで、その日は終了しました。
教室のお友達も、みんなこの数の多さに圧倒され・・・。
そう、でもここからが勝負なんですよー。
どんぐり問題にはこんな仕掛けが沢山あって、子どもたちが
どんな反応をするか観察できるようになっています。
しかも、この問題は連立方程式の問題なので
小学生が単純に計算で出そうとしても
解答には絶対に辿り着きません。
そう、絵で考えなければ答えは出ないように
仕組まれているのです。ふふふ・・・。
でも、裏を返せば、中学生で習う連立方程式の
問題でも、絵を描く事で小学生でも
解けるということなのです。しかも、自力で・・・。
完璧に理解して・・・。
で、その後・・・
問題に関係あるのかないのか・・・
やたらと、30×30は?60×60は?と言うので、
毎日一問、どんぐり方式で解いていました。
どうやら、まだ
3×3=9に0をくっつければよいということに
気付いていないようです。
0くっつけるだけだよ。って教えてもいいのですが、
本人に絵で解いてもらって、納得して欲しいと思ったので
あえて教えないことにしました。
ある夜、
母「明日、どんぐり問題するけど、どの問題がいい?
何でも、いいよ。この前のする?嫌なら何でもいいから他の選んで。」
というと、
息子「じゃあ、この前の続きする。」
母「この前の続きする!偉いね。」
息子「なんで?」
母「だって、お母さんだったら、解けないから他のに
すると思うから。」
「間違った問題とか、二度と見たくない人だったからね。」
「一回、宿題貰って、全然分からんで、手も足もでなくて、
悔しくて、悲しくなって、泣いて、問題破ったことあるしね。」
息子「それ、何年生の時?」
母「5年生のとき。」
息子「えっ!5年生。5年生で問題破る。それ、ちょっと
アホチンだよね。1年生のときかと思った。ははは。」
母「うん、アホチンだよね。ははは。」
ということで、息子大うけ。
次の日
問題を解きました。
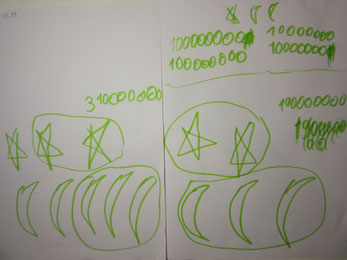
同じ部分を囲っていますね。
いい感じですが、しばらくして終了
さて、今後の経過はどうなりますでしょうか?
進化10 3年かかりました。
さて、今日次男が以下の問題を解いていたのですが、そういえば
長男もまだ正解になってなかったなーと思い、一緒にすることに
しました。
1mx08
マッキー[まっきい]と ラッキー[らっきい]は おちばひろいを しをています。マッキー[まっきい]は 3ぽ あるくたびに 2まい、[らっきい]は 2ほ あるくたびに 1まいの おちばを ひろうことが できます。では、2人[ふたり]あわせて ちょうど 14まいの おちばを ひろうには なんぷん かかるでしょう。2人[ふたり]とも あるく はやさは 1ぽで 1ぷん かかります。2人[ふたり]は いっしょに スタートします。

どうしても24分だー。と言い張る長男に。
でも、二人合わせて14枚の落ち葉を拾うには何分かかるでしょう。
二人とも1歩で一分かかります。二人は一緒にスタートします。って
書いてあるからね。
という文章を
「だって、ほら24でしょ。」
と言ってくる度に、くり返し読み・・・
(基本は一回だけしか読めません。)
結局
最後は泣きながら
鼻水たらしながら
しわくちゃの顔で
恥ずかしそうに、
笑顔で
12分ということに気が付きました。
約3年かかりましたね。
この問題は本当にいい問題なので、皆さんも是非
ヒントを出さずにこどもが自力で解答に至るのを
忍耐強く見守りましょう。
ちなみに、次男は一生懸命何やら書いて、
あー、僕まだこんなにしないといけない。
と、頑張って絵を描いていました。
こちらも、まだあと数年かかる模様です。笑

進化11 どんぐり問題が算数の問題ってことに気が付いてなかった!?
タイトルにもあるように
長男は、
最近までどんぐり問題が算数の問題だということに
気付いていなかったらしい・・・
ホントかよっ!?
って、思わずツッコミ入れてしまいましたが、
どうやら本当らしいです。
「お母さんが言わなかったら、まだ気付いてなかった。」
そうです。
ということで、
とうとう、
この3年生の冬休みに長男のどんぐり問題にも初めて
計算式が登場しました。
以下、2年生の進化3で紹介した団子虫の問題です。
2mx57 ダンゴムシのお母さんが、9ユーロで子ダンゴムシ3匹に、同じお菓子を10個ずつ買ってあげようと思っています。お釣りが出ないように買うと、1個いくらのお菓子を買えばいいのでしょう?

去年は、一個だいたい、いくらくらいかなと見当をつけていって、
何度かやり直して正解していましたが(ノートの左側)、
今回は30個お菓子の絵を描いたところで、9ユーロ÷30に
すればいいということになりました。
もしくは、
3ユーロ÷10でもいいよねということでした。

他には、
2mx67
サンタさんが、子ども4人に、それぞれ同じ値段のお菓子を2個ずつと、
そのお菓子1個の丁度3倍の値段がする玩具を一つずつ買ってあげようと
思っています。ただし、サンタさんが使えるお金を全部で88ユーロとすると、
1個いくらのお菓子と一ついくらの玩具を買ってあげればいいでしょう。
以前までは、こんな感じで大変そうだったんですが・・・
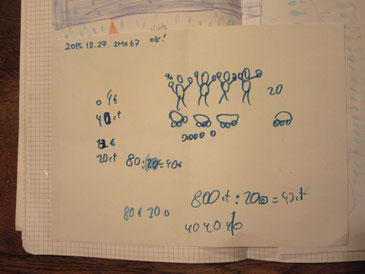
ようやく、理解と計算式がつながりました。
丁度いいころですね。
5歳からどんぐり問題を始めて、
これまでは、理解と思考の部分を重点的に鍛えてきました。
そして、その方法が習慣化され、定着してくるのが
9歳の壁を超える、小学3年生あたりです。
また、
この頃になると子どもたちの抽象思考力が上がってくる
こととも関係しているのだと思いますが、
問題の全体を見渡しながら、細部を考えるということが
上手に出来るようになってくるため、
処理能力が上がります。
打てば響く的な感じです。
この時期までに、しっかりと具象(半具象)思考で思(視)考力鍛えてきた
子どもたちは、小学校4年生頃から学習の内容が少々難しく
なってきても、びくともしない学力を手にいれることが出来ます。
さあ、小学生後半では、これまで鍛えた理解と思考の
過程を算数語(計算式)で表わすことにより、
誰にでも自分の思考過程を分かってもらえるように、
プレゼンテーション力を鍛えていきましょう。
これから、どんぐり問題に取り組まれる方、
なかなか進まないと焦ってしまう方、
大丈夫です。
子どもたちは必ず進化しますので、
どんぐり問題の約束事を必ず守って
丁寧に進めていって下さい。
進化12 まだまだ割り算は使わない!?
3mx43
マッコウクジラのマッコー君とザトウクジラのザットー君が片道50000kmの太平洋往復競争をしました。マッコ―君は1時間に100km、ザット―君は1時間に80km泳げるとするとゴールにたどり着く時間の差はどれくらいになりますか。

50000キロの往復競争ということで、大変な数になっていますが、
マッコウ君の方は、100km╱時が1000回分ということで、1000時間
というところはすぐでたのですが、
ザット―君の80km╱時をどうするか?
ちょっと考えて
80km╱時が1000回分(1000時間)で、80000km
だよね・・・。
100000kmまで
あと、20000kmどうしよう・・・。
うーん・・・。
ということで、
一日目は終了しました。
さて、翌日、
後20000km
あー、
80km╱時×200時間=16000km
80km╱時×50時間=4000km
で、20000kmになるー。
ということは、
全部で、
1250時間かかる
だから、
マッコ―君 1000時間
ザット―君 1250時間
ということで、250時間の差
になり、正解でした。
こんなに数が多くなっても、
割り算なしでも何とかなるもんなんですね。
50000÷80=?って突然するよりも、
このように分解して考えると
簡単に、しかも間違えずに出来ますよね。
身の丈にあった考え方と手順で
よく出来ました。
最初から、
道のり÷速さ=時間のような公式に当てはめた
やり方を教えるとか・・
やはり、あまり関心しませんね。
自分でオリジナルの絵を描いて
そこから、工夫して答えをだすことで
本当の理解が生まれてくるのですから。
進化13 でもそれだけでは問屋が卸しません。同じ問題に見えても全く違う、恐るべしどんぐり問題!
さて前回、進化12で出てきたクジラの往復競争の問題ですが、まだまだ続きがあります。
今回は、
3MX78
マッコウクジラのマッコー君とザトウクジラのザットー君が片道50000kmの太平洋往復競争をしました。マッコ―君は1時間に100km、ザット―君は1時間に90km泳げるとするとゴールにたどり着く時間の差はどれくらいになりますか。
前回の問題と太字の所一か所だけ違うんですが、
これが似て非なるものなり。

さて、息子
前回同様に、マッコ―君は1000時間とすぐにでました。
そして、ザット―君は1111時間ということにして、
(端数を勝手に切り捨てたな!!!)
そして、二人がゴールする時間差は、
111時間という答えになりました。
でも、違います。
で、次に112時間という答えになりました。
それでも、違います。
そして、
だって、90km割れないもーーーーん!!!
と言い訳する。
じゃあ、どうする???
うーーーーーん・・・・・・。
ヒントはもちろん出してはいけません。
で・・・、
1時間は60分でしょ・・・。
あっ、ほらね、ちゃんと考えれるでしょ。
そんな怠慢はゆるされませんよ。心中のつぶやき
なにやら、いろいろ考えていましたが・・・
頭が気もち悪い・・・・。
だって、あと10kmが・・・・。
(ザットー君の99990kmまでは、90km╱時で
割り切れるのですが、残りの10kmは分・秒単位で考える必要が
あるため)
と言い出して、
はい、私にも聞こえてましたよ、その音が
頭の中がバキバキいってましたね。笑
ちなみに答えは、
111時間6分40秒です。
いやー、良く頑張ってると思うよ。
もう、今日は止めといたら。
で、
この日は終了しました。
この様に、どんぐり問題は一見似ている問題が結構出てくるのですが、
よーくみてみると難易度が全く違うんですよね。
また、前学年の問題が次の学年に繰り越されていたりもしますが、
これも、ちゃんとした意図があります。
意図の一つには、子どもの思考力の段階によって、その時々によって解き方が全く違ってくるのでそれを楽しむためということがあります。
また、あえて難しい問題を最初に見せておくことで(解かせることとか正解させることが目的ではない)、子どもの頭に無意識的に、長期的なスパンで準備をさせておくという意図もあります。で、次の学年で同じ問題をもう一度見たときに、自然に免疫がついているんですね。
そう、予防接種みたいなものですね。
今までにないような難しい問題を初めてみたときとか、
明らかに自分では対処できないようなものに出会った時は、
「げっ!」
って、思いますよね。誰でも。
でも、あえてそこで
無理やり果敢にぶつかっていく必要はないんですよ。
だって、準備出来てないから、玉砕します。
もちろん、それを強制してはいけません。
とりあえず、こんなのもありますよ。って見せておいて、
こどもも、あー、こんなのもあるんだって思ってもらって
心構えとそれをどう対処するべきかっていうことを
準備させるんですよね。
そうやって、見続けていると、慣れて来るし、抵抗感が少なくなるんですよね。それが当たり前になりますからね。
すると、準備が出来たときに、
ちょっと戦ってみるかな。と思えるようになり、
そのうちに倒すことが出来るようになります。
ということで、
今回は、どんぐり問題の奥深さについてお話してみました。
さあ、この問題の続きはどうなることでしょうか、
あと10kmをどうするか???
楽しみですねー。
進化14 どうして気が付かないのか?それは数字の罠
はい、今回は以下の問題です。
3mx40
クジラのマッコウ君の今日の朝ご飯はプランクトンです。赤プランクトンと青プランクトンを合わせると12428匹います。赤プランクトンは青プランクトンの丁度12倍だとすると、赤プランクトンと青プランクトンは、各々何匹いるでしょう。
この問題の鍵は、「赤いプランクトンは青いプランクトンの12倍です。」
この部分をしっかり理解して、キチンと丁寧に絵に出来るかどうかです。
次の写真を見て下さい。

ちょっとずるして、というかおおちゃくして、絵で描く所を
12という数字で描いてしまいました。
そうすると、どうなると思いますか?
その12という数字に引っ張られて、よく理解せず考えもせず
12428匹を12で割ってしまいます。
そして、永遠に計算を繰り返すことになるのですが、
答えには当然たどり着けません。
絵をキチンと描かずに12と数字で描いてしまった
たったこのことが、障害になり理解と思考を
妨げてしまうのです。
このような、一見あまり重要でなさそうなことを
キチンと絵に描いていくという習慣こそが学力を
伸ばす上で非常に重要なことになってきます。
ということで、
先ほどの絵をこう描いたらどうでしょうか?

この様に絵を描いて、この絵をずーっと良く見て見るんです。
そうすると、自動的に次にどうすれば良いか見えますよね。
12428匹を●に分配すればよいということを。
そして、その●の数は13です。
これは、些細なことに見えますが、この本のちょっとしたことが
理解と思考に大きな違いを産みます。
国語の文章読解でも同じことが言えます。分かっているようで分かっていないのは、このような細かなところが正確にイメージ化出来ていないからなのです。
ですから、まず大切なことは
文章に書かれている通りに、きちんと絵にする。
そして、自分の描いた絵をよーく見る、見る、見る。
そして、もしその時に気が付かなくても、
ビジュアルイメージを脳にインプットしておきさえ
すれば、
数か月後には自然に脳味噌が答えを出してくれる
ということです。
また、絵を描く理由ですが、頭の中の視覚イメージを大量に長時間保持しておくのは大変なエネルギーを要します。それでは、イメージ保持だけで精一杯で、それを使って思考するのは困難です。ですから、紙に描くのです。そうすることで、視覚イメージ保持に使われるエネルギーを全て考えることに使えますので、少ないエネルギーで多くの思考が可能になるというわけです。

 『どんぐる教室』
inルクセンブルク
『どんぐる教室』
inルクセンブルク
























